이번 글에서는 deep learning 에서 아주 중요한 back propagation 에 대한 insight를 얻기 위해,

Yann LeCun 외 3명이 참여한 1998년 논문 “Efficent BackProp” 을 부분적으로 리뷰해보겠습니다.

다운로드 링크

이 링크 에서 논문 다운받아보실 수 있습니다.

총 10개의 챕터로 구성된 이 논문은

3장까지 간단하게 simple gradient descent 을 통한 Back Propagation 을 설명하고,

4장에 몇가지 트릭들(Few Tricks) 들을 통해 그 성능을 높이는 방법들을 제시하고 있습니다.

저는 제가 관심이 있었던 이 4장의 내용, 즉

“Back Propagation 으로 학습하는 모델들의 학습 성능을 높이는 Trick 들”

을 집중적으로 리뷰해보려고 합니다.

(저희가 요즘 다루는 거의 대부분의 모델들은 back propagation 으로 학습하는 모델이므로 의미가 있습니다)

논문 4장까지의 챕터 구성은 아래와 같습니다.

1. introduction

2. Learning and Generalization

3. Standard Back Propagation

4. Few Practical Tricks

4-1 Stochastic vs Batch Learning

4-2 Shuffling the examples

4.3 Normalizing inputs

4.4 The Sigmoid

4.5 Choosing Target Value

4.6 Initializing Weight

4.7 Choose Learning Rate

(논문의 뒷 내용이 궁금하신 분들은 직접 다운받아서 읽어보시기 바랍니다)

Back Propagation 과 그 방식으로 학습하는 모델의 구조(Neural Network 등) 을 아신다면,

“4. Few Practical Tricks” 을 다루는 단원으로 바로 넘어가셔도 좋습니다.

일반적인 gradient-based 학습 모델

(2 .Learning and Generalization)

---

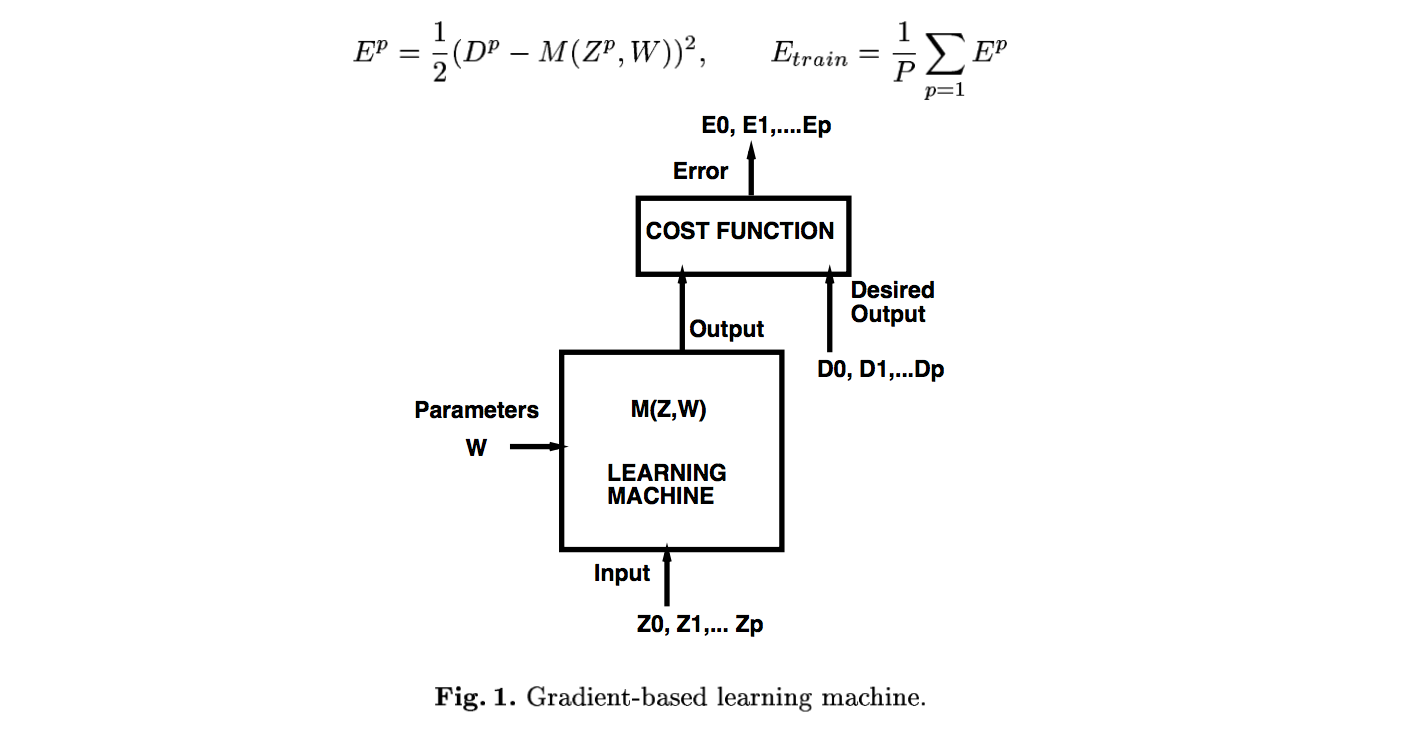
이 논문에서 이야기하는 모델의 모습입니다.

(이런 구조를 가지는 학습 모델은 이 논문에서 말하는 trick들로 성능을 향상시킬 수 있다는 말이겠죠?)

처음 입력값, 즉 input 은 Z 로 표현하였고,

학습 가능한 Parameter 인 W 가 있고 ,

모델에 W, Z가 들어가면 output M(W,Z) 가 나옵니다.

output M(W,Z) 와 desired output D 를 (이 논문에서 말하는) 가장 일반적인 cost fuction 인

mean-square 를 이용하여 E 를 산출하였습니다.

E (error) 는 모델의 성능을 평가하는 유일한 스칼라값입니다.

E (error) 의 값이 작을수록, 모델이 잘 학습했다고 말할 수 있습니다.

즉, 머신 러닝에서의 가장 중요한 부분은

cost function 을 통해 나온 저 E(error) 값을 줄이는 방법을 찾는 일이라고 해도 과언이 아닙니다.

위와 같은 Gradient-based 학습 모델은 이 error 을 줄이는 일을

Back Propagation 이라는 과정을 통해 수행하게 됩니다.

( 그 과정에서 Gradient 가 쓰이기 때문에 Gradient based 학습 모델이라고 부르는 것입니다. )

기본적인 Back Propagation

(3 . Standard Back Propagation)

---

요즘엔 Back Propagation 을 효과적으로 빠르게 수행해주는 방법들이 많이 나와있습니다.

저도 아직 그 종류들과 작동 방식들을 잘 몰라서, 참고 링크를 가져왔습니다.

<다양한 Back="" Propagation="" 알고리즘들="">

http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html

이 글에서는 간단히 Back Propagation 의 작동 방식을 보고 넘어갈 것이기 때문에,

가장 기본적인 Gradient descent 알고리즘 을 통해 back propagation을 살펴보겠습니다.

---

Back Propagation 은 학습 모델에서의 W(trainable parameter) 를 업데이트 하는 방법입니다.

W의 값을 업데이트해서 cost function 의 결과값인 error 가 작아지게 하면 성공입니다.

이 W의 업데이트과정(back propagation) 을 수백번, 수천번 반복해서 천천히 error를 줄여나가는 것입니다.

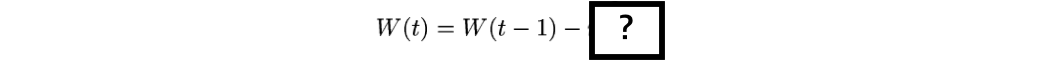
그렇다면 W 를 얼마씩 업데이트 해주어야 할까요?

(그 방법으로 지금까지 많은 사람들이 다양한 알고리즘을 찾아내었고, 그것이 바로 위에 소개해드린 링크의 내용입니다. )

가장 기본적인 Gradient Descent에서는 이전의 W_(t-1) 이 이 모델의 error 에 미친 영향을 편미분을 통해 계산해서,

그 값을 업데이트값으로 사용합니다.

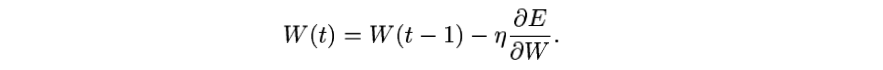(E 는 cost function 의 결과값)

업데이트 값을 구하는 식은 아래와 같습니다.

---

조건

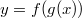
에서의 y의 x 에 대한 편미분을 구하는 식은

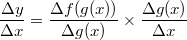
입니다.

---

마찬가지로 조건

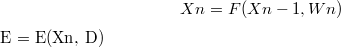
에서의 E 의 Wn에 대한 편미분을 구하는 식은

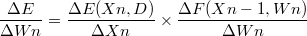
이와 같습니다.

천천히 살펴보시면

기호	의미	편미분 공식 매칭
Wn	n-th layer 의 weight	x
Xn	n-th layer 의 output	g(x)
E(Xn, D)	…	f(g(x))
E	모델의 error	y

이해가 되실 겁니다.

---

같은 방법으로 n-1 번째 layer 의 Wn-1 이 error 에 미친 영향을 구하면 아래와 같습니다.

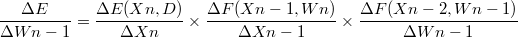
편미분의 연속입니다.

이와같은 방법으로 n-th layer(Wn), n-1-th layer(Wn-1) , … , 2nd layer(W2), input layer(W1) 에 대해

E 에 대한 각각의 편미분을 구해줍니다.

그리고 그 편미분 값을 업데이트 값으로 각각의 W 에 대해 아래 연산을 해줍니다.

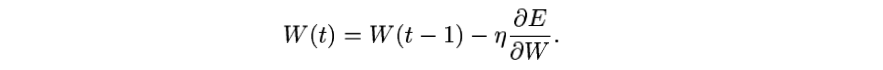
t는 학습 반복횟수고, 몇번째 layer 의 W 인지는 생략되어있습니다.

여기서 저 업데이트 값 앞의 상수는 learning rate 로,

이 값을 어떻게 지정하느냐에 따라 학습의 효과가 달라집니다.

이 값을 조정하는 방법도 4장의 trick에서 다룹니다.

t값이 학습 반복 횟수라고 말씀드렸는데,

이렇게 W 를 업데이트 하는 과정을 수백 수천번 반복하여 t를 올리면, E 는 점점 줄어들게 되고, 모델은 학습을 잘 하게 됩니다.

이것이 기본적인 Back Propagation 을 통한 학습 모델의 학습방법입니다.

(메인) Back Propagation 으로 학습하는 모델들의 학습 성능을 높이는 Trick 들

(4. Few Practical Tricks)

---

4-1 Stochastic vs Batch Learning

4-2 Shuffling the examples

4.3 Normalizing inputs

4.4 The Sigmoid

4.5 Choosing Target Value

4.6 Initializing Weight

4.7 Choose Learning Rate

다음 포스트들에서는 이제 이런 학습 모델들의 학습 성능을 높일 수 있는 trick 들을

개별적인 포스트를 통해 자세히 살펴보겠습니다.

감사합니다.

(질문이나 잘못된 부분 지적은 환영입니다.)